Polarisasie is een van die basiese eienskappe van antennas. Ons moet eers die polarisasie van vlakgolwe verstaan. Dan kan ons die hooftipes antennapolarisasie bespreek.
lineêre polarisasie
Ons sal die polarisasie van 'n vlak elektromagnetiese golf begin verstaan.
'n Planêre elektromagnetiese (EM) golf het verskeie eienskappe. Die eerste is dat die krag in een rigting beweeg (geen veld verander in twee ortogonale rigtings nie). Tweedens, die elektriese veld en die magnetiese veld is loodreg op mekaar en ortogonaal op mekaar. Elektriese en magnetiese velde is loodreg op die rigting van vlakgolfvoortplanting. As voorbeeld, beskou 'n enkelfrekwensie-elektriese veld (E-veld) wat deur vergelyking (1) gegee word. Die elektromagnetiese veld beweeg in die +z-rigting. Die elektriese veld is gerig in die +x-rigting. Die magnetiese veld is in die +y-rigting.
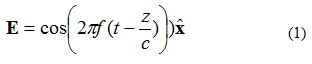
In vergelyking (1), let op die notasie: . Dit is 'n eenheidsvektor (’n vektor van lengte), wat sê dat die elektriese veldpunt in die x-rigting is. Die vlakgolf word in Figuur 1 geïllustreer.
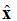
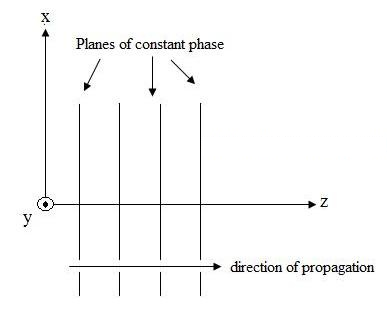
figuur 1. Grafiese voorstelling van die elektriese veld wat in die +z-rigting beweeg.
Polarisasie is die spoor- en voortplantingsvorm (kontoer) van 'n elektriese veld. Beskou as voorbeeld die vlakgolf-elektriese veldvergelyking (1). Ons sal die posisie waarneem waar die elektriese veld (X,Y,Z) = (0,0,0) is as 'n funksie van tyd. Die amplitude van hierdie veld word in Figuur 2 op verskeie tye in tyd geteken. Die veld ossilleer teen frekwensie "F".
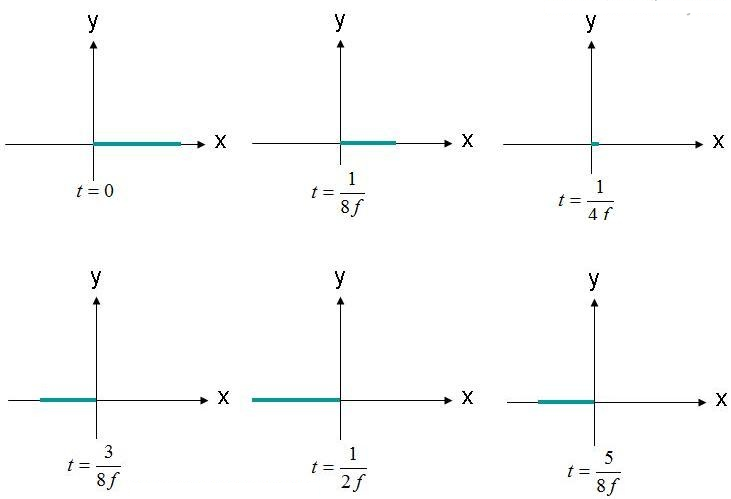
figuur 2. Neem die elektriese veld (X, Y, Z) = (0,0,0) op verskillende tye waar.
Die elektriese veld word by die oorsprong waargeneem en ossilleer heen en weer in amplitude. Die elektriese veld is altyd langs die aangeduide x-as. Aangesien die elektriese veld langs 'n enkele lyn gehandhaaf word, kan hierdie veld lineêr gepolariseer word. Daarbenewens, as die X-as parallel met die grond is, word hierdie veld ook as horisontaal gepolariseer beskryf. As die veld langs die Y-as georiënteer is, kan die golf vertikaal gepolariseer word.
Lineêr gepolariseerde golwe hoef nie langs 'n horisontale of vertikale as gerig te wees nie. Byvoorbeeld, 'n elektriese veldgolf met 'n beperking wat langs 'n lyn lê soos getoon in Figuur 3, sal ook lineêr gepolariseer wees.
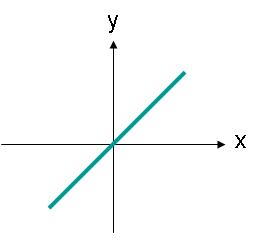
beeld 3. Die elektriese veldamplitude van 'n lineêr gepolariseerde golf waarvan die trajek 'n hoek is.
Die elektriese veld in Figuur 3 kan beskryf word deur vergelyking (2). Daar is nou 'n x- en y-komponent van die elektriese veld. Beide komponente is ewe groot.
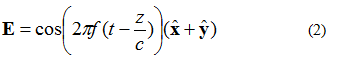
Een ding om op te let oor vergelyking (2) is die xy-komponent en elektroniese velde in die tweede stadium. Dit beteken dat beide komponente te alle tye dieselfde amplitude het.
sirkelvormige polarisasie
Neem nou aan dat die elektriese veld van 'n vlakgolf gegee word deur vergelyking (3):
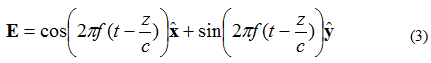
In hierdie geval is die X- en Y-elemente 90 grade uit fase. Indien die veld weer soos voorheen as (X, Y, Z) = (0,0,0) waargeneem word, sal die elektriese veld teenoor tyd-kromme verskyn soos hieronder in Figuur 4 getoon.
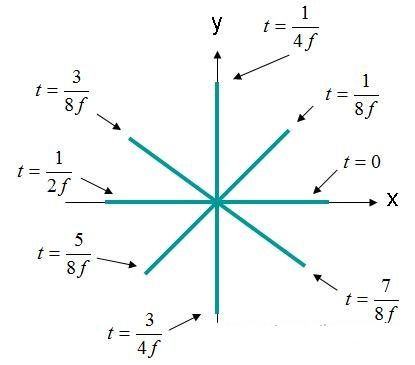
Figuur 4. Elektriese veldsterkte (X, Y, Z) = (0,0,0) EQ-domein. (3).
Die elektriese veld in Figuur 4 roteer in 'n sirkel. Hierdie tipe veld word beskryf as 'n sirkelvormig gepolariseerde golf. Vir sirkelvormige polarisasie moet aan die volgende kriteria voldoen word:
- Standaard vir sirkelvormige polarisasie
- Die elektriese veld moet twee ortogonale (loodregte) komponente hê.
- Die ortogonale komponente van die elektriese veld moet gelyke amplitudes hê.
- Die kwadratuurkomponente moet 90 grade uit fase wees.
Indien dit op die Golf Figuur 4-skerm beweeg, word gesê dat die veldrotasie antikloksgewys en regshandig sirkelgepolariseerd (RHCP) is. Indien die veld kloksgewys geroteer word, sal die veld linkshandig sirkelgepolariseerd (LHCP) wees.
Elliptiese polarisasie
As die elektriese veld twee loodregte komponente het, 90 grade uit fase maar van gelyke grootte, sal die veld ellipties gepolariseer wees. As ons die elektriese veld van 'n vlakgolf in die +z-rigting beskou, soos beskryf deur Vergelyking (4):
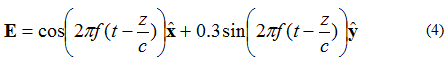
Die lokus van die punt waar die punt van die elektriese veldvektor sal aanneem, word in Figuur 5 gegee.
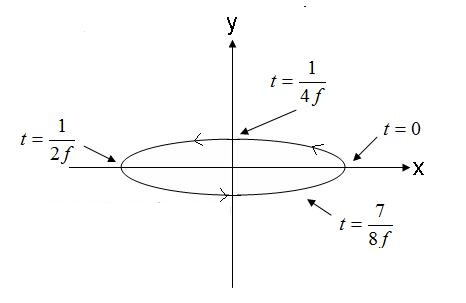
Figuur 5. Prompt elliptiese polarisasiegolf elektriese veld. (4).
Die veld in Figuur 5, wat in 'n antikloksgewyse rigting beweeg, sal regshandig ellipties wees as dit uit die skerm beweeg. As die elektriese veldvektor in die teenoorgestelde rigting roteer, sal die veld linkshandig ellipties gepolariseer wees.
Verder verwys elliptiese polarisasie na sy eksentrisiteit. Die verhouding van eksentrisiteit tot die amplitude van die hoof- en newe-asse. Byvoorbeeld, die golfekssentrisiteit van vergelyking (4) is 1/0.3 = 3.33. Ellipties gepolariseerde golwe word verder beskryf deur die rigting van die hoofas. Die golfvergelyking (4) het 'n as wat hoofsaaklik uit die x-as bestaan. Let daarop dat die hoofas teen enige vlakhoek kan wees. Die hoek is nie nodig om by die X-, Y- of Z-as te pas nie. Laastens is dit belangrik om daarop te let dat beide sirkelvormige en lineêre polarisasie spesiale gevalle van elliptiese polarisasie is. 1.0 eksentriese ellipties gepolariseerde golf is 'n sirkelvormig gepolariseerde golf. Ellipties gepolariseerde golwe met oneindige eksentrisiteit. Lineêr gepolariseerde golwe.
Antennepolarisasie
Noudat ons bewus is van gepolariseerde vlakgolf elektromagnetiese velde, word die polarisasie van 'n antenna eenvoudig gedefinieer.
Antennepolarisasie 'n Antenne-verveld-evaluering, die polarisasie van die resulterende uitgestraalde veld. Daarom word antennas dikwels as "lineêr gepolariseerde" of "regshandige sirkelvormig gepolariseerde antennas" gelys.
Hierdie eenvoudige konsep is belangrik vir antennakommunikasie. Eerstens, 'n horisontaal gepolariseerde antenna sal nie met 'n vertikaal gepolariseerde antenna kommunikeer nie. As gevolg van die wederkerigheidstelling, stuur en ontvang die antenna op presies dieselfde manier. Daarom stuur en ontvang vertikaal gepolariseerde antennas vertikaal gepolariseerde velde. Daarom, as jy probeer om 'n vertikaal gepolariseerde horisontaal gepolariseerde antenna oor te dra, sal daar geen ontvangs wees nie.
In die algemene geval, vir twee lineêr gepolariseerde antennas wat relatief tot mekaar geroteer is met 'n hoek ( ), sal die kragverlies as gevolg van hierdie polarisasie-wanverhouding beskryf word deur die polarisasieverliesfaktor (PLF):
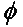
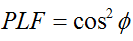
Daarom, as twee antennas dieselfde polarisasie het, is die hoek tussen hul stralende elektronvelde nul en is daar geen kragverlies as gevolg van polarisasie-wanpassing nie. As een antenna vertikaal gepolariseer is en die ander horisontaal gepolariseer is, is die hoek 90 grade, en geen krag sal oorgedra word nie.
LET WEL: Deur die foon oor jou kop na verskillende hoeke te beweeg, word die ontvangs soms verbeter. Selfoonantennas is gewoonlik lineêr gepolariseer, dus kan die draai van die foon dikwels ooreenstem met die polarisasie van die foon, wat die ontvangs verbeter.
Sirkulêre polarisasie is 'n wenslike eienskap van baie antennas. Beide antennas is sirkulêr gepolariseer en ly nie aan seinverlies as gevolg van polarisasie-wanpassing nie. Antennas wat in GPS-stelsels gebruik word, is regshandig sirkulêr gepolariseer.
Neem nou aan dat 'n lineêr gepolariseerde antenna sirkelvormig gepolariseerde golwe ontvang. Neem ook aan dat 'n sirkelvormig gepolariseerde antenna probeer om lineêr gepolariseerde golwe te ontvang. Wat is die gevolglike polarisasieverliesfaktor?
Onthou dat sirkelvormige polarisasie eintlik twee ortogonale lineêr gepolariseerde golwe is, 90 grade uit fase. Daarom sal 'n lineêr gepolariseerde (LP) antenna slegs die sirkelvormig gepolariseerde (CP) golffasekomponent ontvang. Daarom sal die LP-antenna 'n polarisasie-wanpassingsverlies van 0.5 (-3dB) hê. Dit is waar, ongeag die hoek waarteen die LP-antenna gedraai word. daarom:
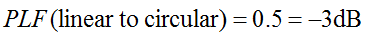
Polarisasieverliesfaktor word soms na verwys as polarisasie-doeltreffendheid, antenna-wanpassingsfaktor of antenna-ontvangsfaktor. Al hierdie name verwys na dieselfde konsep.
Plasingstyd: 22 Desember 2023







